ДВОЙНЫЕ ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ

Введение

В данной работе речь пойдет о системах накопления энергии, состоящих из двух подсистем. Одна подсистема в такой системе накопления энергии основная, другая подсистема дополнительная. Общая структура системы такова, что при введении энергии в основную энергетическую подсистему в дополнительной подсистеме также “наводится” некая энергия. В работе рассматривается поведение двойной энергетической системы с точки зрения обмена энергии между её частями, а также обмена энергией всей системы с внешним исходным источником энергии. Приводятся мысленные примеры.

Определение двойной энергетической системы

Будем считать, что:

1. Двойная энергетическая система накопления энергии состоит из двух подсистем: основной подсистемы и дополнительной подсистемы.

2. При введении энергии в основную подсистему от источника первоначальной энергии в дополнительной подсистеме также появляется “наведенная” энергия, величина которой может быть как больше, так и меньше энергии в основной энергетической системе.

3. Появление “наведенной” энергии в дополнительной системе не требует дополнительных энергетических затрат от источника первоначальной энергии.

4. Убывание энергии в основной энергетической подсистеме приводит к убыванию “наведенной” энергии в дополнительной энергетической системе.

5. Дополнительная энергетическая система может совершать положительную работу, в результате которой проявляется наведенная в ней энергия, при этом уровень энергии в основной энергетической системе может падать, оставаться неизменным, или даже увеличиваться.

6. После потребления энергии от двойной энергетической системы накопления энергии она способна возвращаться в исходное состояние.

7. Все преобразования энергии внутри двойной энергетической системы и обмен энергией с источником первоначальной энергии происходит с потерями, то есть КПД преобразования видов энергии всегда меньше единицы.

Предложенное определение двойной энергетической системы носит абстрактный характер, из которого трудно определить, зачем оно было введено, а также понять возможность физического существования подобных систем в окружающем мире. При этом термин “наведенная” энергия в определении двойных энергетических систем наводит на мысль о возникновении “энергии из неоткуда”, что мешает физическому пониманию введенного понятия. Тем не менее, продолжим рассмотрение подобных систем.

Введем некоторые обозначения.
Е0 – энергия источника первоначальной энергии;
Е1 – энергия основной энергетической системы;
Е2 – энергия дополнительной энергетической системы;
Е3 – энергия в основной системе, появившаяся за счет работы дополнительной;
Е4 – энергия на выходе появившаяся за счет работы дополнительной системы;
К1 < 1 – КПД преобразования энергии от источника к основной системе;
К2 < 1 – КПД преобразования энергии от системы к потребителю;
-1<К3 < 1 – КПД преобразования энергии от дополнительной к основной системе;
К4 < 1 – КПД совершаемой дополнительной системой работы;
0<N>1 – коэффициент наведения энергии в дополнительной системе.

Обратим внимание на то, что N может принимать положительные значения от значений больших нуля до бесконечности. То есть, “наведенная” энергия может быть много больше энергии в основной энергетической системе (например, как реактивная мощность при резонансе).

При N=0 система перестает быть двойной, наведенная энергия отсутствует.

Представим в виде блок – схемы состояние двойной системы при накоплении и отдаче энергии на Рис.1.

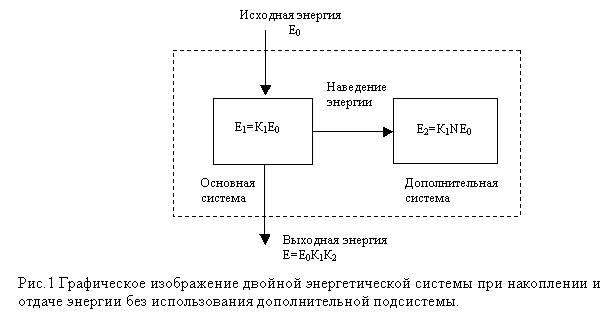
Без использования энергии дополнительной подсистемы поведение подобной системы при накоплении и отдаче энергии ни чем не отличается от поведения обычной одинарной системы, наличие дополнительной подсистемы и энергии в ней никак не проявляется.

Проявить наличие энергии в дополнительной подсистеме можно, совершая работу за счет энергии дополнительной подсистемы.

Двойная энергетическая система устроена так, что совершение работы за счет энергии дополнительной подсистемы должно приводить к изменению энергии основной системы (по определению двойной энергетической системы) и получению наведенной в дополнительной системе энергии в иной форме (как результат работы). Работа по изменению энергии основной системы может совершаться с неким коэффициентом полезного действия К3, который может принимать значения от –1 до +1. При отрицательных значениях коэффициента, энергия основной системы убывает, при положительных значениях возрастает.

Кроме изменения энергии основной системы, работа, являясь преобразователем одного вида энергии в другой, должна приводить к получению энергии Е4 с неким коэффициентом полезного действия К4 – Рис.2.

Энергия в подобной энергетической системе может зацикливаться, путем подачи энергии с выхода в исходный накопитель. При полном удалении энергии из двойной системы в исходный накопитель, энергии в ней не остается. Система в отсутствии энергии возвращается в исходное состояние (по определению), то есть ее части совершавшие работу возвращаются в исходное состояние.

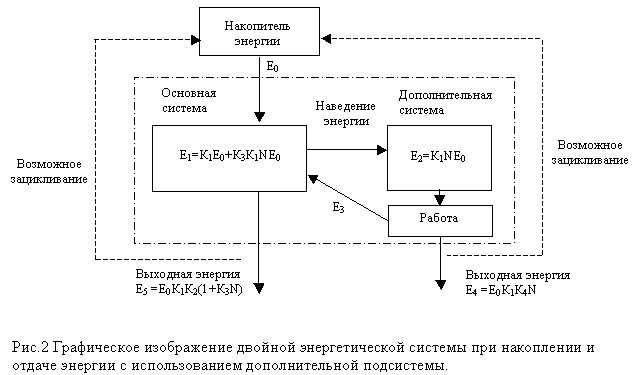
Таким образом, при использовании дополнительной энергетической подсистемы энергия на выходе будет отличаться от энергии на выходе без ее использования. Наиболее интересен случай, когда энергия на выходе превышает энергию на входе. При этом все энергетические преобразования совершаются с потерями.

Условие получения дополнительной энергии на выходе можно записать в виде коэффициента увеличения энергии Кe = Е/E0 >1

Кe = К1К2(1+N(К3+К4)) > 1 (1)

При выполнении условия (1) и подаче энергии с выхода системы на ее вход – Рис.2, зацикливание процесса должно приводить к неограниченному росту энергии. При этом преобразование энергии внутри системы идет с потерями, а подвода дополнительной энергии извне не требуется.

Энергия Еi на выходе системы после i – го цикла равна

Еi =Е0Кie (2)

В виде графика эта зависимость отображена на Рис.3.

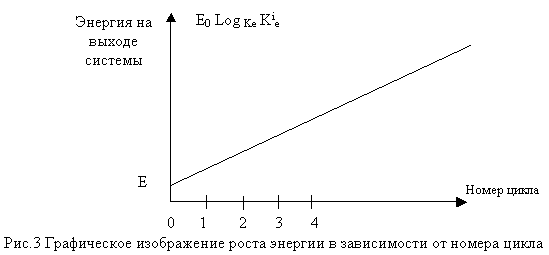
При этом между циклами двойная система возвращается в исходной состояние в условиях отсутствия в ней энергии. То есть, все части системы, совершавшие работу, возвращаются в исходное состояние. Рабочий цикл двойной системы в этом случае можно описать следующим образом:

1. Введение энергии в систему от источника накопления первоначальной энергии;

2. Совершение работы;

3. Удаление результирующей энергии из системы в источник первоначального накопления энергии;

4. Возврат системы в исходное состояние при отсутствии в ней энергии;

5. Повторение цикла.

Однако, приведенное описание двойных энергетических систем является не более чем абстракцией. Существование подобных систем в реальном мире требует подтверждения. Кроме того, слабым местом, с точки зрения физики, при описании модели двойной энергетической системы является понятие “наведения” энергии без дополнительных затрат со стороны источника энергии.

Подобное поведение двойной системы казалось бы должно противоречить закону сохранения энергии и первому началу термодинамики. Поэтому, без иллюстрации физического смысла введенных понятий дальнейшие рассуждения будут малоинтересными.

Наиболее близко, с физической точки зрения, определение двойных энергетических систем сопоставимо с движением материального тела по замкнутой траектории в потенциальном поле, когда производимая работа равна нулю.

Движение тела по замкнутой траектории в потенциальном поле

Из курса физики известно, что работа, совершаемая точкой при движении по замкнутой траектории в потенциальном поле, равняется нулю.

Объясняется это тем, что работа, совершаемая силой при перемещении точки из одного произвольного положения 1 в другое произвольное положение 2,

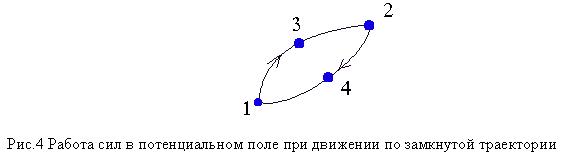
не зависит от траектории перемещения точки в потенциальном поле, т.е. выполняется условие A132 = A142 - Рис. 4.

Таким образом, при перемещении тела из начального положения в конечное положение величина работы одинакова вне зависимости от формы траектории. При обратном движении работа меняет знак на противоположный: A241 = - A142

Следовательно, работа по замкнутому контуру равняется нулю A132 + A241 = 0.

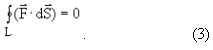
Что абсолютно справедливо для замкнутых энергетических систем, когда отсутствует приток и отток сил в систему.

Если система открытая, то есть существует приток и отток сил, то этот баланс сил надо учитывать.

Двойная энергетическая система является открытой системой, поскольку энергия в нее то закачивается, то выкачивается. Следовательно, работа, совершаемая вдоль траектории А132, не равна работе совершаемой вдоль траектории А142, если при движении вдоль одной траектории поле присутствует, а при движении по другой траектории поле отсутствует.

Необходимо только создавать и удалять поле в необходимые моменты времени, что оказывается достаточно просто в электротехнике.

Электрическое поле конденсатора можно убрать, разрядив конденсатор на сверхпроводящую катушку без потерь, а магнитное поле катушки можно убрать, зарядив конденсатор от сверхпроводящей катушки. При этом интервал времени между первым и вторым событием может быть достаточно большим для перемещения материальной точки из одной точки траектории в другую точку.

При этом, если принять во внимание наличие источника накопления первоначальной энергии, то систему в целом можно рассматривать как замкнутую, поскольку отсутствует подвод дополнительной энергии извне.

Таким образом, для двойных энергетических систем энергия потенциального поля является энергией основной системы, а потенциальная энергия точки в поле энергией дополнительной системы. Без самого потенциального поля не может быть потенциальной энергии точки в поле. При этом, движение точки в поле можно совершать, а можно и не совершать, оставляя энергию точки в потенциальном виде. При этом, работа будет как совершаться, так и не будет совершаться в зависимости от наличия и отсутствия поля.

Отличие в рассмотрении двойных систем и работы точки в потенциальном поле заключается в том, что энергию потенциального поле при анализе движения точки в поле обычно не учитывают в балансе энергий.

Для более детальной физической иллюстрации понятия энергии и рассмотрения возможности реализации двойной энергетической системы проведем мысленный эксперимент.

Мысленный эксперимент с воздушным конденсатором

Эксперимент состоит в оценке емкости и энергии воздушного конденсатора, заряженного до некоторого напряжения, до и после само - произвольного сближения обкладок, вызванных притяжением разноименных зарядов.

Этап 1
Оценим параметры конденсатора при начальном положении обкладок.
Заряд конденсатора Q емкостью С при напряжении U равен

Q= CU (4)

Энергия Ес конденсатора равна

Еc = CU2/2 (5)

Емкость С конденсатора с плоскими пластинами равна

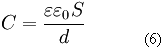
где:
S - площадь обкладок конденсатора
d – расстояние между обкладками конденсатора
е0 – диэлектрическая проницаемость вакуума
е – относительная диэлектрическая проницаемость воздуха, близкая к единице.

Этап 2
Допустим, что само - сближение обкладок вызвало уменьшение расстояния между ними в N раз. Уменьшение расстояния между обкладками в N раз приводит к повышению емкости конденсатора в N раз, что при сохранении первоначального заряда вызывает падение напряжения на конденсаторе в N раз. Следовательно, при увеличении емкости в N раз энергия конденсатора падает также в N раз.

Следовательно, проводимая обкладками конденсатора при их сближении работа приводит к падению энергии конденсатора, так как напряженность электрического поля падает. Приведенный эксперимент хорошо знаком из курса физики.

Следовательно, данная двойная энергетическая система не приводит к увеличению энергии в процессе работы дополнительной подсистемы, поскольку напряженность электрического поля после проведения работы падает.

Мысленный эксперимент с постоянными магнитами

Эксперимент состоит в оценке энергии магнитного поля одинаковых магнитов до и после их сближения.

Этап 1
Берем N магнитов, расположенных относительно друг друга на расстоянии, позволяющем утверждать, что “взаимного влияния практически нет”.

Из теории магнетизма вспоминаем, что энергия магнитного поля при напряженности Н в объеме V с проницаемостью m в соответствии с классическим определением равна

W = mH2V/8П (7)

Будем считать, с некоторым допущением, что эта энергия и есть энергия отдельного магнита со средней напряженностью магнитного поля Н в объеме V.

Тогда суммарная энергия W1N магнитного поля всех магнитов будет равна

W1N = WN = NmH2V/8П (8)

Этап 2
Сближаем N магнитов, так чтобы они заняли один и тот же объем (на практике этого достичь нельзя – магниты встанут только рядом, но это мысленный эксперимент) при этом направление полюсов совпадает.

Этап 3
Оцениваем энергию результирующего магнита.

В результате “слияния” всех магнитов напряженность магнитного поля HN результирующего магнита увеличится в N раз

HN = NH (9)

То есть, за счет увеличения напряженности поля магнит станет в N раз сильнее.

При этом энергия объединенного магнита W2N, в соответствии с ранее указанной классической формулой (4), станет равной

W2N = WN = N2mH2V/8П (10)

А отношение энергий магнитного поля всех магнитов после сближения W2N к энергии магнитного поля всех магнитов до сближения W1N станет равной

W2N/ W1N =N (11)

То есть, энергия магнитного поля после “слияния” всех магнитов возросла в N по сравнению с суммарной энергией отдельных магнитов.

Откуда взялась дополнительная энергия?
Видимо, дополнительная энергия - это потенциальная энергия взаимного расположения магнитов, которая перешла в энергию магнитного поля объединенного магнита. То есть, магнитное поле, совершая работу, увеличило энергию объединенного магнита. При условии, что все рассуждения правильные.

При этом следует заметить, что магниты сближались сами, без приложения дополнительных сил, следовательно, к ним можно было в принципе подсоединить некое устройство, переводящее производимую ими работу в другой вид энергии, например, электрическую и получить еще дополнительную энергию вдобавок к той, что образовалась в объединенном магните.

Мысленный эксперимент со сверхпроводящими катушками

Эксперимент состоит в оценке энергии одновитковых сверхпроводящих катушек до и после их сближения.

То есть, эксперимент повторяет предыдущий, но вместо постоянных магнитов используются сверхпроводящие одновитковые катушки.

Этап 1
Берем подходящие материалы для создания N сверхпроводящих катушек без сердечника.

Этап 2
Изготавливаем N сверхпроводящих катушек без сердечника, и запитываем их током I.

Этап 3
Располагает катушки относительно друг друга на расстоянии, позволяющем утверждать, что “взаимного влияния практически нет”.

Оцениваем энергию магнитного поля отдельной катушки и суммарную энергию всех катушек.

Как известно, напряженность магнитного поля одного витка с током в его центре равна

H = I/2r (12)

Где
I – ток в одновитковой катушке
r – радиус витка

Эту напряженность поля, усредненную по некоторому объему V, и будем считать определяющей энергию магнитного поля W витка с током (как ранее для постоянных магнитов)

W = H2V/8П (13)

Тогда, суммарная энергия W1N витков с током равна

W1N = WN = NH2V/8П (14)

Этап 4
Сближаем N катушек, так чтобы они заняли один и тот же объем, то есть слились (на практике этого достичь нельзя – катушки встанут только рядом, но это мысленный эксперимент) при этом направление полюсов совпадает.

Тогда величина тока IN в результирующей катушке возрастет в N раз

IN = IN (15)

При этом энергия W2N объединенной катушки , в соответствии с ранее указанной классической формулой (10), станет равной

W2N = WN = N2H2V/8П (16)

А отношение энергий магнитного поля всех катушек после сближения W2N к энергии магнитного поля всех катушек до сближения W1N станет равной

W2N/ W1N =N (17)

То есть, энергия магнитного поля после “слияния” всех катушек возросла в N по сравнению с суммарной энергией отдельных катушек.

При этом замечания относительно дополнительной энергии можно сделать такими же, как и для постоянных магнитов.

Мысленный эксперимент со сверхпроводящей катушкой и сердечником

Эксперимент состоит в оценке индуктивности сверхпроводящей катушки без сердечника и с сердечником, а также в определении энергии запасенной катушкой в этих двух состояниях при постоянстве тока.

В процессе мысленного эксперимента производится “зацикливание” системы.

Этап 1
Берем подходящие материалы для создания сверхпроводящей катушки без сердечника.

Этап 2
Изготавливаем катушку без сердечника индуктивностью L, и замораживаем ее до появления сверхпроводимости.

Этап 3
Запитываем изготовленную катушку от внешнего источника , например, конденсатора емкостью С при напряжении U, обладающего энергией Ee

Ee=CU2/2 (18)

Замыкаем катушку и отключаем внешний источник энергии. Получаем таким образом сверхпроводящий электромагнит без сердечника.

Ток I, текущий в катушке на основе закона сохранения энергии равен

Em=LI2/2=CU2/2 (19)

I=sqrt(CU2/L) (20)

Этап 4
Совершаем полезную работу, вводя медленно внутрь катушки ферромагнитный сердечник проницаемостью М. ( Сердечник сам будет втягиваться, занимая положение с наименьшей потенциальной энергией, для механической системы катушка – сердечник, его надо только тормозить, совершая работу, работа будет равна силе умноженной на расстояние.)

Этап 5
Оцениваем индуктивность и энергию поля катушки с ферромагнитным сердечником

Индуктивность по классической формуле возрастет в М раз

Lc=ML (21)

Соответственно увеличится и энергия в М раз

Emc=MLI2/2 (22)

Этап 6
Разряжаем катушку с током на исходный конденсатор. Получаем энергию в конденсаторе в M раз большую первоначальной энергии

Eec=MCU2/2=MLI2/2 (23)

При этом напряжение на конденсаторе будет больше в корень из М от первоначального.

Таким образом, совершая положительную работу в механической системе из катушки и сердечника, можно повысить энергию магнитной системы. При этом магнитная система (катушка с током) является основной подсистемой двойной системы, а механическая система (катушка и сердечник) является дополнительной подсистемой.

В результате проводимой дополнительной подсистемой работы энергия магнитного поля катушки увеличивается.

Этап 7
Если ошибки в рассуждениях нет, то сердечник, закрепленный на пружине, возвращается в исходное состояние, часть заряда конденсатора идет на запитывание катушки вновь, а часть на иную полезную работу. Цикл повторяется до бесконечности, обеспечивая в двух его местах выход дополнительной энергии.

Откуда берется энергия в мысленном эксперименте с катушкой и сердечником?

1. При запитывании катушки током возникает энергия магнитного поля, но одновременно, как бы даром, возникает потенциальная энергия в механической системе катушка – сердечник. На создание этой потенциальной энергии дополнительные затраты не требуются.
2. Общая энергия системы, таким образом, равна сумме энергии запасенной в магнитном поле и потенциальной энергии механической системы.
3. Характер поведения частей системы при совершении работы разный
А. При расходовании энергии магнитного поля катушки, потенциальная энергия механической системы также убывает, вся энергия уходит из системы
Б. При расходовании энергии механической системы энергия магнитного поля возрастает, энергия от механической системы добавляется к энергии магнитного поля катушки, вся энергия остается в системе.
В. Удаление сердечника из катушки происходит при отсутствии энергии в системе и не требует специальных затрат.

Однако, при допущении, что в рассуждениях нет ошибки, и система работает.

Если ошибки в рассуждениях нет то, разряжая конденсатор в конце цикла на катушку без съема дополнительной энергии, получаем взрывной характер протекания процесса, даже без учета механической работы катушка – сердечник.

Так при проницаемости М равной 1*103 (тысяча, что является не проблемой для современных сердечников), через 10 циклов имеем 1*103030 кратное увеличение энергии. Это взрыв.

Замечания по мысленному эксперименту

1. Слабым местом у таких рассуждений может быть уменьшение тока при введении сердечника в катушку. Однако, за счет чего он должен уменьшатся не понятно. Если сердечник вводится медленно, то противо ЭДС не возникает. Скорость введения на величину совершаемой работы не влияет.
2. Обзор сверхпроводящих магнитов показал, что существуют магниты, как с сердечником, так и без него. Главное чтобы сердечник не входил в насыщение – это ухудшает параметры магнита. Если насыщения нет, то все нормально.
3. Если ток в сверхпроводящей катушке не уменьшается при введении сердечника, то других принципиальных причин неработоспособности устройства, видимо, нет.

Таким образом, на примере мы проиллюстрировали что такое “наведенная” энергия в дополнительной подсистеме двойной энергетической системы. В приведенном примере “наведенной” энергией является потенциальная энергия механической системы катушка – сердечник.

Кроме этих примеров, очевидно, возможны и другие.

Например, можно объединить последовательно эксперимент с катушками и эксперимент с сердечником. В этом случае катушки вначале “сливаются”, а затем вводится сердечник.

Или еще, например, две двойные энергетические системы могут работать друг на друга

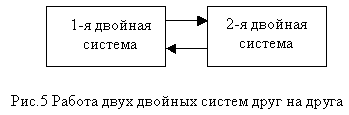
Выводы

Понятие “двойные энергетические системы” является абстракцией, обладающей интересными свойствами. Энергия подобной системы при определенных условиях может неограниченно возрастать. При этом преобразование энергии внутри системы идет с потерями, а подвода дополнительной энергии извне не требуется. Наблюдаемый процесс носит взрывной характер. Физическая реализуемость подобных устройств экспериментально не подтверждена, но мысленные эксперименты, проведенные в работе с некоторыми допущениями, позволяют на это надеяться.

Различие в мысленных экспериментах с конденсатором, магнитами и электромагнитами можно объяснить тем, что при проведении работы конденсатором напряженность электрического поля падает, а при проведении работы магнитами напряженность магнитного поля возрастает.

Однако, противоречие с законом сохранения энергии и первым началом термодинамики ставит реализуемость подобных систем под вопрос.

В то же время, само понятие двойных энергетических систем может быть путем к разрешению этого противоречия, поскольку простейшие существующие системы накопления энергии являются двойными энергетическими системами. Просто в них приняты все меры к тому, чтобы потенциальная энергия не совершала работы, и они оставались одинарными. Кроме того, не обеспечено удаление энергии из системы после совершения работы и возврат системы в исходное состояние.

Литература

Справочник по физике для поступающих в ВУЗы. Авторы: Гаевой А.И., Калабухов Н.П., Левашова Л.Е и др., по редакцией Калабухова Н.П., Издательство “Наукова Думка“, Киев, 1969 год.

Версия для печати
Автор: Уткин В.М., г. Москва
Дата публикации 08.02.2010гг

вверх